 |
Astrophysical gases tend to radiate when heated. This radiation is an energy leak which may carry away substantial amounts of energy. A simulation which does not include the radiative cooling (such as the one in the previous section) is often referred to as an adiabatic simulation.
The file corocool.tab (in anonymous ftp) contains what is called
a coronal cooling curve. The file contains two columns, the
first one lists the log of the temperature, the second one the log of
the cooling ![]() in units of erg cm
in units of erg cm![]() s
s![]() . This particular
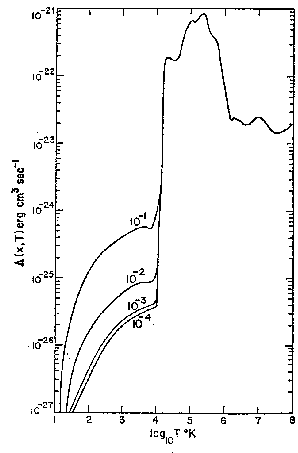
cooling curve is taken from Dalgarno & McCray (1972), reproduced here
as Fig. 3. It was calculated by determining the equilibrium ionization
state at every temperature and from that the amount of emission. Below
. This particular
cooling curve is taken from Dalgarno & McCray (1972), reproduced here
as Fig. 3. It was calculated by determining the equilibrium ionization
state at every temperature and from that the amount of emission. Below
![]() K the cooling depends strongly on the ionization fraction of
the gas, the one in the table is the curve labelled
K the cooling depends strongly on the ionization fraction of
the gas, the one in the table is the curve labelled ![]() in the
paper. The cooling rate of a gas can be approximated by
in the
paper. The cooling rate of a gas can be approximated by
![]() ,
where
,
where ![]() is the number density of particles.
is the number density of particles.
Numerically, the cooling is a source term for the energy density and can be included in a similar way as the geometric source terms, i.e. in a separate calculation every time step. However, there is the danger that the cooling will reduce the temperature/internal energy density below zero, which is unphysical. The reason for this is the very non-linear behaviour of the cooling function. There are two ways to control this:
A) Solve the problem from Section 2 with radiative cooling included. Still assume that all material is ionized. What differences are there with the non-cooling solution? Why is the effect larger for the outer shock than for the inner shock? Is it possible to resolve the cooling region? What compression (density jump) do you find for the swept up shell?
If you are unsuccessful in getting the code to run with cooling, you
can try lowering the overall density. This will reduce the cooling
rate. You could for instance try
![]()
![]() yr
yr![]() and
and
![]()
![]() yr
yr![]() for the fast and slow wind
respectively. A 10 times lower density gives a 100 times lower
cooling. If you reduce the density too much the result of the
calculation will be the similar to the one without cooling.
for the fast and slow wind
respectively. A 10 times lower density gives a 100 times lower
cooling. If you reduce the density too much the result of the
calculation will be the similar to the one without cooling.
B) Follow the interaction between a moderately fast wind and an outer
slow wind. Use the following parameters:
![]()
![]() yr
yr![]() ,
, ![]() km s
km s![]() for the
fast wind, and
for the
fast wind, and
![]()
![]() yr
yr![]() ,
,
![]() km s
km s![]() for the slow wind. First do a simulation without cooling
and then add the cooling. Compare the two results and also compare them to
the differences between the non-cooling and cooling simulation for the
1000 km s
for the slow wind. First do a simulation without cooling
and then add the cooling. Compare the two results and also compare them to
the differences between the non-cooling and cooling simulation for the
1000 km s![]() wind. Why is the behaviour of the inner shock very
different?
wind. Why is the behaviour of the inner shock very
different?
C) A weakly cooling bubble is often called energy conserving and a strongly cooling bubble momentum conserving. Lamers & Cassinelli (1999) state in Sect. 12.3 of their book that one can observationally check whether a bubble is momentum or energy conserving by considering the following ratios:
![]() =(total kinetic energy in shell)/(total wind energy
provided)
=(total kinetic energy in shell)/(total wind energy
provided)
![]() =(momentum in the shell)/(momentum imparted by the wind)
=(momentum in the shell)/(momentum imparted by the wind)
If
![]() the shell is energy conserving, whereas when
the shell is energy conserving, whereas when
![]() it is momentum conserving.
it is momentum conserving.
Check whether the shells in your models are indeed energy
conserving and momentum conserving according to these
definitions, by calculating ![]() and
and ![]() for both cases.
for both cases.