


Next: Boundary conditions
Up: Making a hydrodynamics code
Previous: Choosing the time step
The source terms fall outside the Roe solver formalism. It is in fact
possible to integrate them into the Roe solver but we will not do that
here. Instead we will use an approach called operator splitting.
It is possible to show that an equation
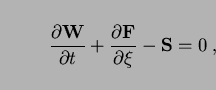 |
(17) |
can be numerically solved (to second order accuracy) by solving for
each time step the two separate equations
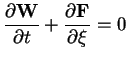 |
|
|
(18) |
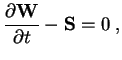 |
|
|
(19) |
after each other. The first equation is dealt with by the Roe solver
routine, the second one you will have to write an integration routine
for. Since it is an ordinary differential equation, standard methods
can be used. Do not use a very fancy method however, realise that both
the Roe solver and the splitting are only second order accurate, so it
is not necessary to be more accurate than that when solving Eq. (19).
One can show that a more accurate (but perhaps unnecessary) approach
to the splitting is to integrate Eq. 19 over
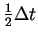 ,
then Eq. 18 over
,
then Eq. 18 over 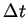 , then Eq. 19 over
, then Eq. 19 over
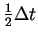 again. This is known as Strang splitting.
again. This is known as Strang splitting.



Next: Boundary conditions
Up: Making a hydrodynamics code
Previous: Choosing the time step
Garrelt Mellema
2003-01-20
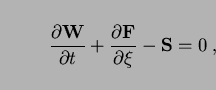
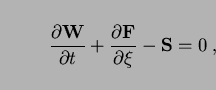
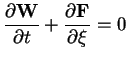
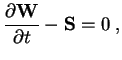
![]() ,
then Eq. 18 over
,
then Eq. 18 over ![]() , then Eq. 19 over
, then Eq. 19 over
![]() again. This is known as Strang splitting.
again. This is known as Strang splitting.