Problem Set for Stellar Structure and Evolution

Garrelt Mellema
Stockholm Observatory

April/May 2000

1. Apparent and absolute magnitudes

Show from the definition of magnitudes that the difference between two apparent magnitudes is equal to the difference between the two corresponding absolute magnitudes: $m_{1}-m_{2}=M_{1}-M_{2}$ and thus independent of distance.

2. Wien's displacement law

The wavelength at which a blackbody spectrum peaks is given by Wien's displacement law:

$$\lambda_{\rm max}=0.290/T\quad\hbox{\rm cm}\;.$$

Use this to find at which wavelengths the peak of the spectrum lies for the following dwarf stars (luminosity class V) from the stellar data table: B0, A0, G2, K0, M6.

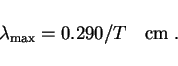
Also find the effective temperatures at which black body spectra peak for the centres of the photometry filters U (365 nm), B (440 nm), V (550 nm), R (700 nm), I (900 nm), and K (2200 nm). (The R, I and K filters are a continuation of the UBV system to infrared wavelengths). Which of the filters are best for detecting the 5 spectral types above?

3. Blackbodies

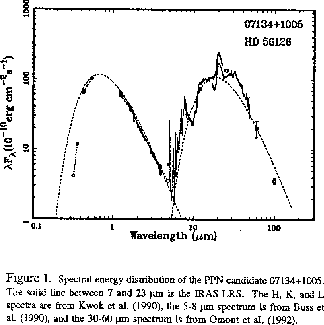
When fitting observations of some stars one finds that one needs two black body curves in order to make a good fit. An example is shown in the figure below. The dotted lines are the fits and the points and solid lines are the observations. Find the effective temperatures for the two curves using the wavelength at which they peak. What might be going on here? (hint: stars cannot be cooler than about 2,000 K; notice that in the observations the blue part of higher temperature black body lies below the fit, i.e. some of this radiation is `missing').

4. The linear stellar model

Derive the linear stellar model for a star of mass $M$ and radius $R$ by assuming that the density varies with radius as

$$\rho(r)=\rho_{\rm c}(1-r/R).$$

and solving the equations of mass conservation and hydrostatic equilibrium. A complete model consists of $M_r$ and $P$ as functions of $r$, and expressions for $\rho_{\rm c}$ and $P_{\rm c}$. Using the ideal gas law, also derive expressions for $T_{\rm c}$ and $T$ as a function of $r$.

Compare the values of $\rho_{\rm c}$, $P_{\rm c}$, and $T_{\rm c}$ with the Sun: $P_{{\rm c},\odot}=2.50\times 10^{17}$ dynes cm$^{-2}$ (the unit for pressure in the cgs system, 1 dyne cm$^{-2}$ = 0.1 Pa), $T_{{\rm c},\odot}=1.58\times 10^7$ K, $\rho_{{\rm c},\odot}=162$ g cm$^{-3}$, $X_{{\rm c},\odot}=0.35$ and $Z_{{\rm c},\odot}=0.02$?

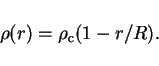
5. Molecular weights

Find the mean molecular weight $\mu$ for the case of fully ionized pure hydrogen: $X=1$, $Y=Z=0$. Explain why it has this value. Do the same for fully ionized pure helium ($Y=1$, $X=Z=0$) and solar abundances ($X=0.7$, $Y=0.28$, $Z=0.02$).

6. Mean molecular weight per electron

Apart from the usual mean molecular weight $\mu$, one often also defines a mean molecular weight per electron $\mu_{\rm e}$, so that

$$n_{\rm e}={\rho \over \mu_{\rm e} m_{\rm H}}\,.$$

For the case of complete ionization, show that

$$\mu_{\rm e} \simeq {2 \over 1+X}\,.$$

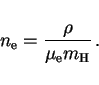
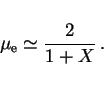
7. Effect of composition differences

In the later faces of stellar evolution the stellar core may have a different chemical composition than the stellar envelope. Assume that the transition from the core to the envelope is sharp. In equilibrium the pressure and temperature need to be constant across this surface. Show that a density jump must be the result. If the core is pure He and the envelope pure H, by which fraction must the density change?

8. Degeneracy

Use the definition of the Fermi energy to derive the approximate density at which electron degeneracy becomes important for temperatures of $10^7$ K (hint: take $\epsilon\sim {3\over 2}kT$).

Neutrons are also fermions with spin 1/2, but with a mass of $1.7\times 10^{-24}$ kg. At approximately which density do the neutrons become degenerate?

9. Degeneracy pressure

A numerical expression for the degeneracy pressure of non-relativistic electrons is

$$P^{\rm deg}_{\rm e}=9.9\times 10^{12} (\rho/\mu_{\rm e})^{5/3}$$

in which the units are cgs and $\mu_{\rm e}$ is the mean molecular weight per free electron, equal to $2/(1+X)$ (see problem 6).

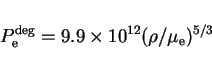
Estimate the density (expressed as $\rho/\mu_{\rm e}$) at which the degeneracy pressure $P^{\rm deg}_{\rm e}$ of the non-relativistic electrons becomes larger than their contribution to the gas pressure $P^{\rm g}_{\rm e}$. What is the value for for $P^{\rm deg}_{\rm e}/P^{\rm g}_{\rm e}$ in the centre of the Sun where $T_{{\rm c},\odot}=1.58\times 10^7$ K, $\rho_{{\rm c},\odot}=162$ g cm$^{-3}$, $X_{{\rm c},\odot}=0.35$ and $Z_{{\rm c},\odot}=0.02$?

10. Dynamic time scales

a. Put the pressure term in the equation of motion (Eq. 10.6) at the surface of the star to zero and estimate the dynamical time scale (also called the hydrostatic time scale) from the equation of motion. What is the value for the Sun?

b. The balance between the gravitational force and the pressure gradient in a star is very delicate. This can be seen by considering the case of a small deviation from hydrostatic equilibrium near the surface of the Sun, say by a factor of 0.01%, so

$${{\rm d}P\over {\rm d}r} = -(1-10^{-4}){GM\rho \over r^2}.$$

Using the equation of motion to estimate the time for a change in radius of 10% (use surface values for quantities dependent on radius).

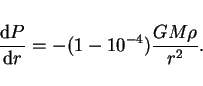
c. Consider the case of a pressure-less sphere of radius $R$ collapsing under its own weight $M$. Solve the equation of motion to find the time scale for complete collapse (the so called free fall time $t_{\rm ff}$).

Hint: multiply the equation of motion by ${\rm d}r/{\rm d}t$ and integrate once. Integrate once more (over radius) to find the time scale. The integral can be solved by substituting $r=R\cos^2u$.

What is the expression for $t_{\rm ff}$ if the sphere has a constant density $\rho_0$?

11. Gravitational time scales

a. For a star with total mass $M$, radius $R$ and a mass distribution $M_r$, write down the gravitational potential at a radius $r$. The total gravitational energy $U_{\rm g}$ can be found by integrating over the entire star. Do this for the case of a star of constant density $\rho_0$ and for the case of a star with a linear density law:

$$\rho(r)=\rho_c(1-r/R).$$

On the basis of this give an estimate for the total gravitational energy of the Sun. If the Sun's energy would be produced by gravitational collapse, how long would its life be? This time scale is called the Kelvin-Helmholtz time scale.

b. Assuming that the Sun produces its luminosity by releasing gravitational energy, estimate its yearly change in size. The precision with which we can currently measure the solar radius is about $0^{\prime\prime}.1$. How long would it take before we could notice a change in size?

Up to the beginning of this century is was believed that the Sun produces its energy by gravitational collapse, leading to a discrepancy between geological and biological times and the solar evolution time.

12. Major nuclear burnings

The full expression for the energy production rate per unit of mass (in W/kg) for the pp-cycle, CNO-cycle and $3\alpha$ processes are given by

$$\epsilon_{\rm pp}= 2.36\times 10^2 \rho X^2 \psi T_6^{-2/3} e^{-33.81/T_6^{1/3}},$$ (1)

$$\epsilon_{\rm CNO}= 8.71\times 10^{23} \rho X X_{\rm CNO} T_6^{-2/3} e^{-152.28/T_6^{1/3}},$$ (2)

$$\epsilon_{3\alpha}= 5.09\times 10^7 \rho^2 Y^3 T_8^{-3} e^{-42.94/T_8},$$ (3)

with $\rho$ the mass density, $X$, $Y$ and $X_{\rm CNO}$, the H, He, and combined CNO abundances, $T_n$ the temperature in units of $10^n$ K. The factor $\psi$ for the pp-cycle depends on the importance of the different branches.

a. Explain why the $3\alpha$ rate depends on the $\rho^2$ whereas the rates for the pp and CNO cycles only depend on $\rho$. Give also a suggestion why the exponents for the temperature terms in the $3\alpha$ rate differ from those in the pp and CNO cycle rates.

b. Calculate the ratio of the energy generation rate for the pp chain to the energy generation rate for the CNO cycle given conditions characteristic of the centre of the present day Sun: $T_{\rm c}=1.58\times 10^7$ K, $\rho_{\rm c}= 162$ g cm$^{-2}$, $X=0.34$, and $X_{\rm CNO}=0.013$. Take $\psi$ to be 1.

c. Derive power law approximations for $\epsilon_{\rm pp}$ and $\epsilon_{\rm CNO}$ around $T=10^7$ K and for $\epsilon_{3\alpha}$ around $T=10^8$ K by considering ${\rm d}\ln \epsilon/{\rm d}\ln T$. Using these power laws, calculate how much the $\epsilon$s change for temperature variations of 1%, 5%, and 10%.

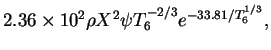13. Radiation pressure

Using the results for the central pressure and temperature from the linear model (problem 4), estimate for which stellar parameters radiation pressure becomes more important than gas pressure in the core.

14. Kramer's opacities

Explain why in the Kramer's opacities the free-free opacity is proportional to $(1+X)(X+Y)$, the bound-free to $(1+X)Z$, and the electron scattering to $(1+X)$ (Consider which type of particles play a role in these sources of opacity).

15. Eddington limit

Show that in the case of heat transfer by radiative diffusion the temperature gradient implies a gradient in the radiation pressure. This gradient equals the radiant heat flow.

Bearing in mind that a pressure gradient corresponds to a force on the gas, find the radiant heat flow which by radiation pressure alone can support the atmosphere of a star with surface gravity $g=GM/R^2$. From this show that there is a maximum luminosity for a star of mass $M$ above which radiation pressure will push away the atmosphere:

$$L_{\rm max}=4{\pi}cGM/\kappa$$

where $\kappa$ is the opacity of the atmosphere.

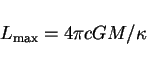
Obtain a numerical estimate for $L_{\rm max}$ by assuming that the surface is hot enough for electron scattering to be the dominating source of opacity. Express $M$ in solar masses ( $M_\odot=2\times 10^{30}$ kg).This maximum luminosity is called the Eddington limit.

16. Polytropic models

Using the expression from the notes on polytropic models show that for a polytropic model of order $n$

$$R\propto \rho_{\rm c}^{{(1-n)\over 2n}}$$

and

$$M \propto R^{{3-n \over 1-n}}$$

Show that this last expression implies that for a star whose pressure is dominated by non-relativistic electrons its volume is inversely proportional to its mass.

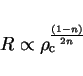
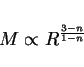
Also show that for a star whose pressure is dominated by extremely relativistic electrons there is only one possible solution for the mass.

Use the full equation of state for relativistic electrons and the equations for a polytrope to derive an expression for this solution.