



Next: Method of calculations
Up: Theory of relativity
Previous: Schwarzschild holes
Contents
Kerr holes
Most of the astrophysical objects rotate, so we expect most black holes formed
by gravitational collapse to be rotating. The Kerr black hole is rotating, and
it is axially symmetric but not spherically symmetric. This solution of
Einstein's equations, discovered in 1963 by R. Kerr (1963), was not at first
recognized to be a black hole solution.
The most general stationary black hole metric, with parameters mass  , angular
momentum
, angular
momentum  , and electric charge
, and electric charge  , is called the Kerr-Newman metric.
A Kerr hole is the special case when
, is called the Kerr-Newman metric.
A Kerr hole is the special case when  . Black holes in nature are expected
to have
. Black holes in nature are expected
to have  , since matter on a macroscopic scale is neutral. Written in the
, since matter on a macroscopic scale is neutral. Written in the
 coordinates of Boyer and Lindquist (1967), which is a
generalization of the Schwarzschild coordinates, the Kerr metric has the form:
coordinates of Boyer and Lindquist (1967), which is a
generalization of the Schwarzschild coordinates, the Kerr metric has the form:
 is the mass of the black hole, and
is the mass of the black hole, and  is its specific angular momentum
divided by
is its specific angular momentum
divided by  . The black hole is rotating in the
. The black hole is rotating in the  direction, and
direction, and
 |
(28) |
In textbooks one often use the so-called geometrical units, a system of units in
which  . In these units, the Schwarzschild radius is
. In these units, the Schwarzschild radius is  .
.  is thus
measured in cm. Here, I will not use the geometrical unit system, but the CGS
system.
is thus
measured in cm. Here, I will not use the geometrical unit system, but the CGS
system.
There is an off-diagonal term in the metric, in contrast to the Schwarzschild
metric:
 |
(29) |
When setting  in equation (27) we get the Schwarzschild metric.
in equation (27) we get the Schwarzschild metric.
The component  in the metric (27), which determines
the rate of flow of time, vanishes at:
in the metric (27), which determines
the rate of flow of time, vanishes at:
or at  , where
, where  is given by
is given by
 |
(30) |
The boundary  is called the static limit (see figure
5). No material bodies
can be at rest within the surface
is called the static limit (see figure
5). No material bodies
can be at rest within the surface
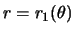 . The reason for this is the same as in the
Schwarzschild field at
. The reason for this is the same as in the
Schwarzschild field at  . Namely, the world line of the observer ceases
to be time-like, as indicated by the reversal of sign of
. Namely, the world line of the observer ceases
to be time-like, as indicated by the reversal of sign of  at
at  .
But an essential difference in comparison with the Schwarzschild field must be
emphasized, because there are some additional features caused by the rotation.
As a massive object spins, it induces a rotation in the surrounding space-time,
a phenomenon known as frame dragging. If
.
But an essential difference in comparison with the Schwarzschild field must be
emphasized, because there are some additional features caused by the rotation.
As a massive object spins, it induces a rotation in the surrounding space-time,
a phenomenon known as frame dragging. If  , all bodies are
unavoidably dragged into rotation, although
, all bodies are
unavoidably dragged into rotation, although  is not the event horizon
because a body may escape from this region. In the metric (27), the
event horizon lies at
is not the event horizon
because a body may escape from this region. In the metric (27), the
event horizon lies at  , that is, at
, that is, at  , where
, where
 |
(31) |
For a rotating black hole, the Boyer-Lindquist coordinates are singular at the
horizon. As in the Schwarzschild case, it requires an infinite time  (measured by an observer at rest far away from the black hole), for any particle
or photon to fall through the event horizon. The dragging of inertial frames
forces particles and photons near the horizon to orbit the black hole with
(measured by an observer at rest far away from the black hole), for any particle
or photon to fall through the event horizon. The dragging of inertial frames
forces particles and photons near the horizon to orbit the black hole with  . Consequently, for a particle falling through the horizon we have that
. Consequently, for a particle falling through the horizon we have that
 and also
and also
 , an infinite twisting of worldlines
around the horizon.
, an infinite twisting of worldlines
around the horizon.
Figure:
Near a rotating black hole, frame dragging is so severe that there is a
nonspherical region outside the event horizon called the ergosphere where
any particle must move in the same direction that the black hole rotates. The
outer boundary of the ergosphere is called the static limit, so named
because once inside this boundary a particle cannot possibly remain at rest
there (i.e., be static) relative to the distant stars.
|
|
The region between the event horizon  and the static limit
and the static limit  is called
the ergosphere. Space-time within the ergosphere is rotating so rapidly
that a particle would have to travel faster than the speed of light to remain at
the same angular coordinate (e.g. at the same value of
is called
the ergosphere. Space-time within the ergosphere is rotating so rapidly
that a particle would have to travel faster than the speed of light to remain at
the same angular coordinate (e.g. at the same value of  in the coordinate
system used by a distant observer).
When
in the coordinate
system used by a distant observer).
When  , the static limit and the event horizon coincide, there is
no dragging of inertial frames; there is no ergosphere.
, the static limit and the event horizon coincide, there is
no dragging of inertial frames; there is no ergosphere.
There is an upper limit of  for a black hole to form, namely
for a black hole to form, namely
If the black hole spins so fast that this constraint is violated, the centrifugal
forces, will exceed the gravitational forces and halt the collapse. For a Kerr
hole where  , this implies that the spin of the black hole must be
, this implies that the spin of the black hole must be
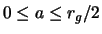 . A black hole with
. A black hole with  is called an extreme Kerr hole. The
event horizon for an extreme Kerr hole is situated at
is called an extreme Kerr hole. The
event horizon for an extreme Kerr hole is situated at  .
.




Next: Method of calculations
Up: Theory of relativity
Previous: Schwarzschild holes
Contents
Juri Poutanen
2000-04-25
![]() , angular
momentum
, angular
momentum ![]() , and electric charge
, and electric charge ![]() , is called the Kerr-Newman metric.
A Kerr hole is the special case when
, is called the Kerr-Newman metric.
A Kerr hole is the special case when ![]() . Black holes in nature are expected
to have
. Black holes in nature are expected
to have ![]() , since matter on a macroscopic scale is neutral. Written in the
, since matter on a macroscopic scale is neutral. Written in the
![]() coordinates of Boyer and Lindquist (1967), which is a
generalization of the Schwarzschild coordinates, the Kerr metric has the form:
coordinates of Boyer and Lindquist (1967), which is a
generalization of the Schwarzschild coordinates, the Kerr metric has the form:
![]() in the metric (27), which determines
the rate of flow of time, vanishes at:
in the metric (27), which determines
the rate of flow of time, vanishes at:


![\includegraphics [scale=0.6]{figkerr.eps}](img198.gif)
![]() and the static limit
and the static limit ![]() is called
the ergosphere. Space-time within the ergosphere is rotating so rapidly
that a particle would have to travel faster than the speed of light to remain at
the same angular coordinate (e.g. at the same value of
is called
the ergosphere. Space-time within the ergosphere is rotating so rapidly
that a particle would have to travel faster than the speed of light to remain at
the same angular coordinate (e.g. at the same value of ![]() in the coordinate
system used by a distant observer).
When
in the coordinate
system used by a distant observer).
When ![]() , the static limit and the event horizon coincide, there is
no dragging of inertial frames; there is no ergosphere.
, the static limit and the event horizon coincide, there is
no dragging of inertial frames; there is no ergosphere.
![]() for a black hole to form, namely
for a black hole to form, namely