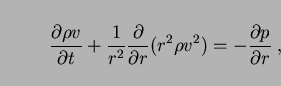Next: Properties of the Euler
Up: Introduction
Previous: Introduction
The behaviour of an ideal compressible gas is described by the Euler equations:
with
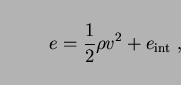 |
(4) |
the internal energy of the gas.
Reducing these to one spatial dimension and using cartesian
coordinates one can write them as
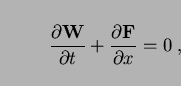 |
(5) |
with 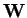 the so called state vector (
the so called state vector (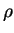 ,
, 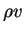 ,
, 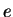 )
)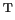 , and
, and
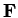 the flux vector (
the flux vector (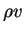 ,
, 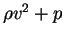 ,
, 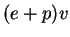
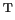 ). The
elements of the state vector are also called the conserved
quantities since the Euler equations basically say that mass,
momentum and energy are conserved. The variables
). The
elements of the state vector are also called the conserved
quantities since the Euler equations basically say that mass,
momentum and energy are conserved. The variables 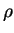 ,
, 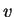 , and
, and 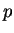 are often referred to as the primitive variables.
are often referred to as the primitive variables.
The Euler equations are not complete without an equation of state. We
choose an ideal gas for which
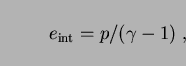 |
(6) |
where 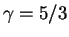 for a monatomic gas, and
for a monatomic gas, and
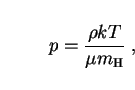 |
(7) |
with 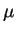 the mean molecular weight.
the mean molecular weight.
A more general form of the Euler equations is
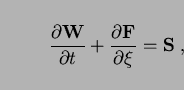 |
(8) |
in which 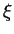 now is an arbitrary spatial coordinate and
now is an arbitrary spatial coordinate and 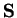 is
the source vector.
is
the source vector. 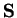 can be split into two parts:
geometrical source terms which arise in the case of non-cartesian
coordinates, and physical source terms such as radiative heating and
cooling, gravitation, etc.
can be split into two parts:
geometrical source terms which arise in the case of non-cartesian
coordinates, and physical source terms such as radiative heating and
cooling, gravitation, etc.
We will be using the spherical coordinate 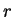 . For this the momentum
equation is
. For this the momentum
equation is
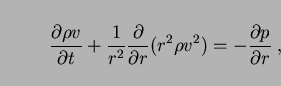 |
(9) |
and similar expressions can be written down for the continuity and
energy equations. To write this in the form of Eq. (8) we take
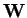 is still the vector of conserved quantities vector since it
is total mass, momentum and energy which are conserved, not their
densities. In spherical coordinates a volume element is proportional
to
is still the vector of conserved quantities vector since it
is total mass, momentum and energy which are conserved, not their
densities. In spherical coordinates a volume element is proportional
to 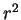 (really
(really
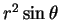 but we are not considering the
but we are not considering the
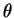 coordinate here), so by multiplying the densities by the
position dependent volume factor
coordinate here), so by multiplying the densities by the
position dependent volume factor 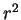 , one obtains the conserved
quantities.
, one obtains the conserved
quantities.
One sees that choosing a non-cartesian coordinate leads to the
appearance of a geometrical source term. There are actually several
ways in which to split off the geometrical source terms, but here we choose
the one shown in Eqs. (10)-(12).



Next: Properties of the Euler
Up: Introduction
Previous: Introduction
Garrelt Mellema
2003-01-20
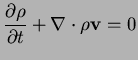
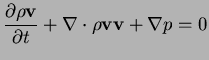
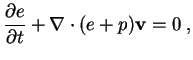
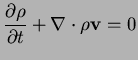
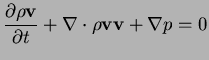
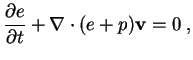
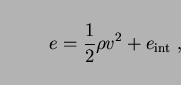
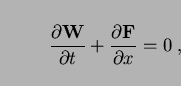
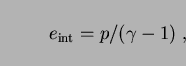
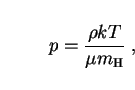
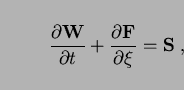
![]() . For this the momentum
equation is
. For this the momentum
equation is