


Next: Numerical approach
Up: Introduction
Previous: The Euler equations
The Euler equations are a simpler version of the Navier-Stokes
equations. The latter contain terms for the viscosity and thermal
conductivity of the gas. In astrophysics these are normally not
thought to be important.
Using the Euler equations also implies using a fluid approximation,
i.e. the particles interact with each other sufficiently to establish
a Maxwell-Boltzmann distribution. This approximation is mostly valid,
but there are exceptions.
From a mathematical point of view the Euler equations are a set of
non-linear, coupled, hyperbolic differential equations. Hyperbolic
differential equations have two important properties:
- they allow discontinuous solutions; in physical terms this means
that the flow can contain shocks or contact discontinuities.
- one can define so called characteristics or characteristic speeds. These are the eigenvalues of the problem: the
solution can be written in terms of a sum of eigenvectors, three in
the case of a one-dimensional problem. The three eigenvectors are
also called waves and are physically associated with the
characteristic speeds
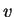 ,
, 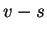 ,
, 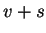 , the velocity of the flow, and
the velocity of sound added and subtracted. The physical relevance of
this is that in a gas no signal can travel faster than the local sound
speed, and
, the velocity of the flow, and
the velocity of sound added and subtracted. The physical relevance of
this is that in a gas no signal can travel faster than the local sound
speed, and 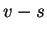 and
and 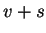 are the highest possible signal speed
within a flow with velocity
are the highest possible signal speed
within a flow with velocity 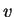 . This also means that the
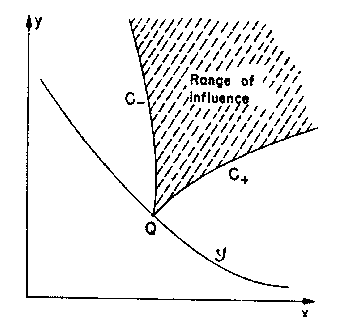
characteristics delineate a domain of influence in space-time (see
Fig. 1). Point Q can only influence the hashed region of space-time.
. This also means that the
characteristics delineate a domain of influence in space-time (see
Fig. 1). Point Q can only influence the hashed region of space-time.
Figure 1:
The domain of influence in the 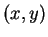 space
space
 |
Physically, shocks can be thought to occur because the particles
suddenly have to adjust to a new situation. There is therefore a close
relation between the characteristics and the shocks: if for example an
explosion occurs at point A, its effect will spread with the
characteristic speeds 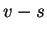 and
and 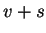 , or in other words
, or in other words 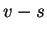 and
and
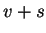 are the shock speeds.
are the shock speeds.



Next: Numerical approach
Up: Introduction
Previous: The Euler equations
Garrelt Mellema
2003-01-20
![]() and
and ![]() , or in other words
, or in other words ![]() and
and
![]() are the shock speeds.
are the shock speeds.